We had ‘computers’ before we had digital computers, a statement that may initially sound strange but is rooted in historical fact. Long before the advent of digital computing devices, the term ‘computers’ referred to individuals—often women—tasked with performing complex mathematical calculations. These ‘female computers’ were highly intelligent and skilled women who worked on intricate mathematical problems, often aiding their male colleagues. This historical context is important as it illustrates the idea that our brains function in ways analogous to a computer, processing and interpreting data.
In fact, when dealing with uncertain situations like football, the human brain may be better equipped to compute the right answer than a digital computer. This superiority is typically found among highly intelligent individuals, or in the specific context of football, among exceptional live scouts. What distinguishes a very good live scout? A top-notch live scout possesses the ability to preview how a player will develop in the future or envision how he might perform in a different team or even in a different league. The term ‘prevision’ is chosen here deliberately, as a replacement for ‘prediction,’ in line with the philosophy of Professor Bruno de Finetti. When people use the word ‘predict,’ it can imply an ability to foretell the future with absolute certainty. Conversely, the term ‘prevision’ conveys a sense of subjectivity, emphasizing that it represents an individual’s personal anticipation of the future rather than a statement of absolute certainty.
The effectiveness of a very good live scout is rooted in his brain’s ability to absorb a wealth of data through live scouting and subsequently compute a prevision. In the case of an exceptional live scout, this prevision tends to be quite close to how reality unfolds in the future. While the very good live scout may not be right every single time, the accuracy of his previsions more often aligns with actual outcomes, demonstrating the superiority of human intuition and analysis in certain contexts.
The supremacy of live scouting stems from the human brain’s ability to process a significantly greater amount of data than current digital computers. What the brain of very good live scouts absorbs in terms of data while watching a live match far exceeds the information available in even the most detailed football statistics or what a video scout can glean from watching the same match on video. The richness and complexity of the data available in the brain of a skilled live scout make their computation of previsions a highly valuable asset. As a result, their insights and judgments often serve as the best and most essential foundation for making recruiting decisions.
Why live scouts still need data
The primary reason why live scouts continue to rely on data scouts is that data scouting enhances the efficiency of live scouting. By employing data scouting, clubs can prioritize and identify the players who are most critical to observe, streamlining the process in a way that is more efficient than relying solely on live scouts. This targeted approach ensures that live scouts focus their attention on the matches that are most important for the club. This synergy between data scouting and live scouting is well recognized, and clubs that utilize data scouting tend to employ it in this manner, maximizing the effectiveness of their scouting efforts.
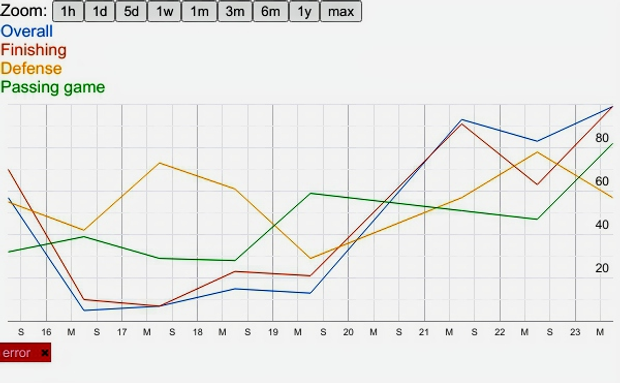
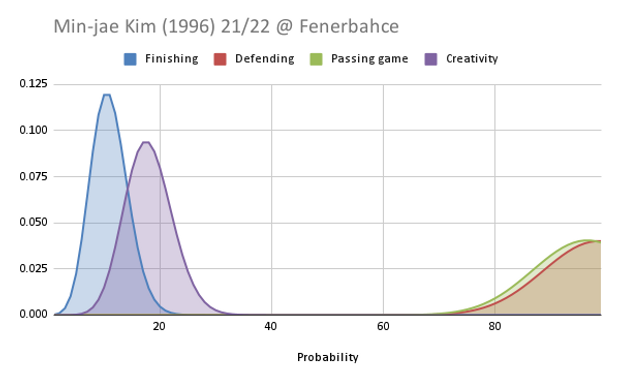
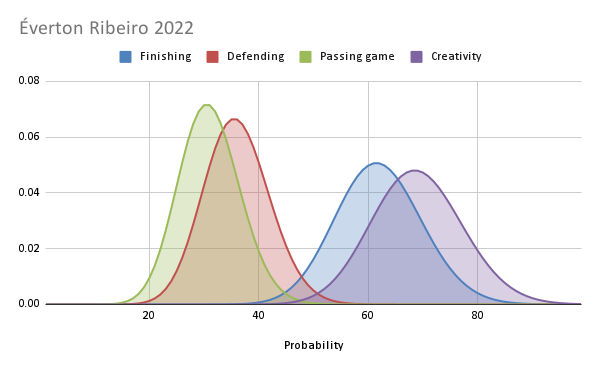
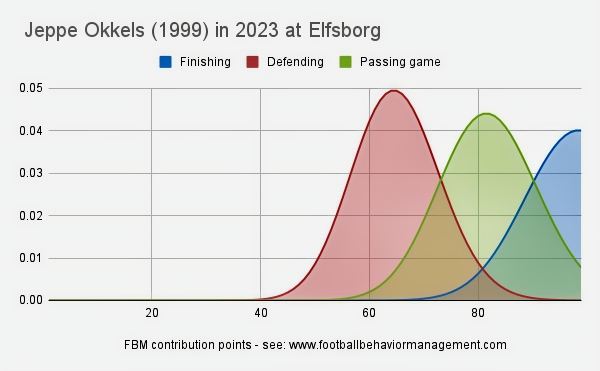
What nearly all clubs overlook, however, is that data can also influence the computation that a live scout makes during live scouting, provided it is presented in a way that is actually useful to the scout. To clarify, most football data fail to assist live scouts in any meaningful way. Even the most visually appealing spider graph fails to provide any valuable insights to a live scout. However, tools like FBM charts and FBM career charts stand out as exceptions, as they can genuinely aid live scouts in understanding the players they are observing. These charts are easily interpretable once their basic principles are understood. Therefore, it is crucial to integrate data, video, and live scouting, acknowledging the unique contribution of each approach, to create a comprehensive and effective scouting strategy.
Finally, data represents another source of subjective judgments about a player, and in the context of risk management, the more varied and independent sources you have, the more robust your risk management becomes. This effectiveness stems from the fact that risk is minimized when all possible sources, provided they are independent, align with one another. When these various perspectives converge, it increases the confidence in the assessment and thereby enhances the decision-making process, reducing the likelihood of misjudgment or oversight
Why a few clubs prefer data over live scouting
Some clubs prefer data over scouting, and the most plausible explanation for this preference is that they may not have yet engaged with a very good live scout or may have had negative experiences with subpar live scouting in the past. Just as exceptional football players are rare, so too are top-tier live scouts. Therefore, it’s crucial for a club to evaluate its scouts. Interestingly, clubs that work with data often amass a considerable amount of information about football players but neglect to gather data on their own scouts. We assist clubs in implementing measuring systems that can either begin evaluating scouts from this point forward or utilize their historical scouting reports as a means to assess how well they have previewed the future of football players. This approach ensures that the evaluation process is comprehensive, taking into account both the potential of the players and the effectiveness of the scouting staff.
In conclusion, live scouting stands as the most crucial form of scouting and should serve as the decisive factor in recruiting decisions. However, to enable live scouts to arrive at more accurate previsions of the future, it’s essential to provide them with football data in a format that their brains can effectively utilize for computation. Tools like FBM charts and FBM career charts are prime examples of how data can be structured to enhance the live scouting process. By integrating these elements, clubs can create a more effective and nuanced approach to scouting that leverages the unique strengths of both live observation and data analysis.