Category: Statistics
-

Unified Scouting Language and AI
Unified Scouting Language is a set of specifications of player behaviors that are in line with the MARCO criteria of Organizational Behavior Management (OBM): Using Unified Scouting Language prevents the scout from overinterpreting what he sees into value judgements, attitudes, generalizations and status. In order to help scouts, especially new scouts, write correctly according to…
-

Why live scouting is the most important … but also why live scouts need data
We had ‘computers’ before we had digital computers, a statement that may initially sound strange but is rooted in historical fact. Long before the advent of digital computing devices, the term ‘computers’ referred to individuals—often women—tasked with performing complex mathematical calculations. These ‘female computers’ were highly intelligent and skilled women who worked on intricate mathematical…
-
Grading players
Grading players comes with a myriad of pitfalls. To begin with: talent is a left skewed distribution like this: What this means is that in professional football the probability of finding a player scoring a 10 is much smaller than finding a player scoring a 1 or a 2. Yt, if you look into the…
-

Did you watch that player?
Fans, if they disagree with FBM stats, often ask me: “Did you actually watch this player?” The short answer is: “No!” That is not my job. My job is to make an assessment of how likely it is that a player is going to contribute to the team. Yet, if you are not a good…
-
FBM Finishing Points
FBM Finishing Points is a predictor of match results. Preliminary results show that FBM Finishing Points predict the correct outcome of a match in 60% of the cases (n=27, p<0.1). In 54% of the cases FBM Finishing Points is a better explanation of the end result than xG and in 50% of the cases FBM…
-
How does FBM replacement values compare to TransferMarkt?
Although FBM replacement values are not meant to predict future transfer fees, it was noticed by many people that often the FBM replacement values of a player were much closer to the actual transfer fee than the valuation listed on TransferMarkt. For that reason we counted in how many cases FBM transfer values were closer…
-
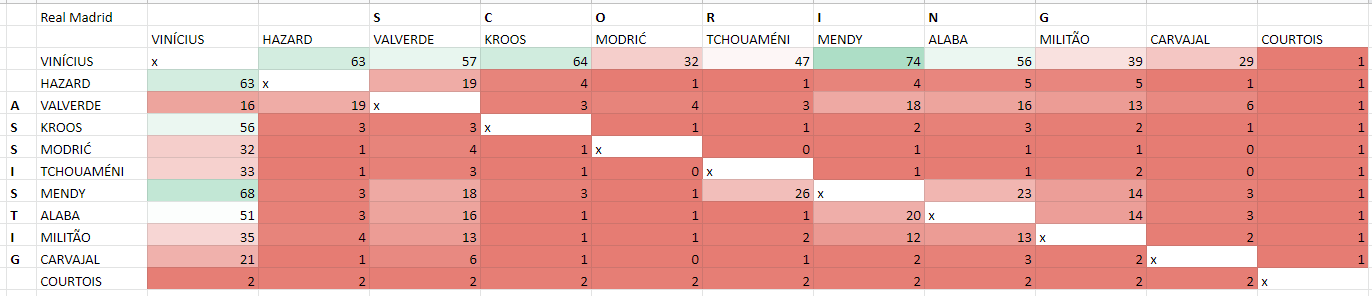
The FBM Bayesian Transfer Model
All data is subjective, no matter how hard proponents of objectivity try to make you think differently. Because all data is subjective a player has different stats for different teams. To think that one set of data describes a player for every team is a simplification that many people are happy to make, because they…
-
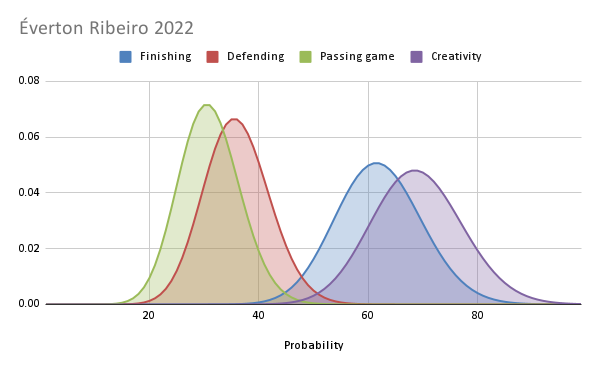
The FBM Creativity stat
Creativity is what cannot be measured by statistics. Hence the difficulty is creating a creativity stat. Nevertheless, we have developed a FBM Creativity stat and tested it. The FBM creativity stat has a p<0.0001 (n=47) to be correct according to the judgment of scouts. Even though the number of participants in the test is small,…
-
Three policies from the Football Behavior Management course that you can implement right away
Football Behavior Management is Organizational Behavior Management (OBM) for football clubs. Here are three smart policies that help strengthen your club immediately: I) Start measuring your scouts, training staff and decision makers Why only use statistics for your players, when statistics works as well – if not better – for scouts, training staff and decision…
-
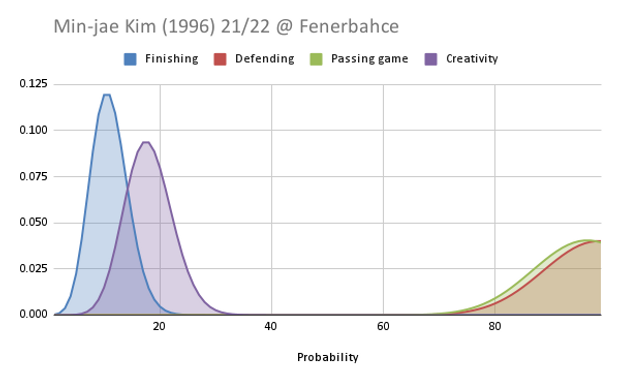
How to read a FBM chart
Maybe you have come across a FBM chart like the following on Twitter and you are curious how to read these charts: DM request: Oscar Fraulo (2003) is a fantastic CM, a superstar in the making. You have seen me complain about CMs a lot, but Fraulo sets the standard on CMs. Maxed out finishing…